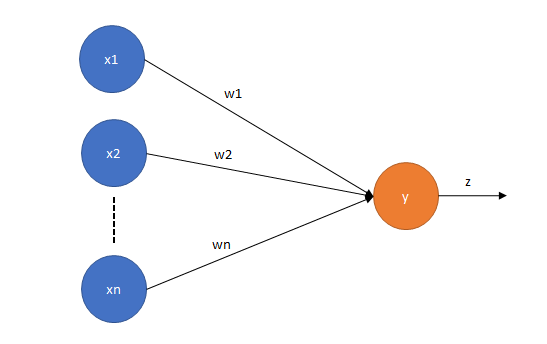
Perceptron Menggunakan Theano

Apakah itu Perceptron?

Perceptron ditemukan oleh Rosenblatt pada tahun 1958 [1]. Perceptron merupakan Artificial Neural Network (ANN) tanpa hidden layer, dimana input layer terhubung langsung dengan output layer. Perceptron merupakan salah satu algoritma linear, sehingga memiliki performa yang tidak cukup baik dalam menyelesaikan permasalah non-linear.

Secara umum perceptron model serupa dengan linear regresi model. Regresi dapat dimodelkan dengan formula:

$y = xb + a$

dimana,

$x = input \\ y = output \\ b = gradient \\ a = konstanta$

Sedangkan perceptron dapat dimodelkan dengan formula

$y = \sum_{n} w_i x_i = W^T x$
$\frac{\partial y}{\partial w_i} = x_i$

dimana,

$x = input\\ y = output \\ W = weights \\ \sigma(.) = output \ function$

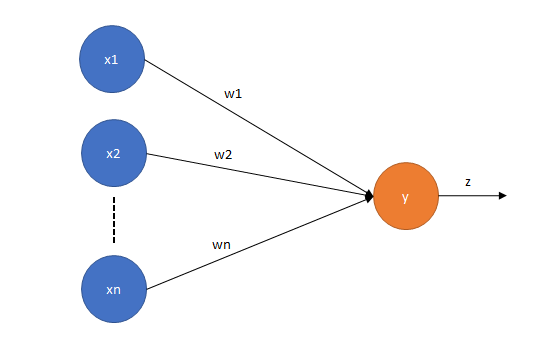
Dikarenakan model perceptron yang sederhana, saya menyarankan agar mempelajari perceptron terlebih dahulu sebelum mepelajari Multiple Layer Perceptron (MLP) atau ANN dengan hiden layer >= 1.

Pada postingan kali ini saya akan membahas mengenai perceptron dan bagaimana cara mentrain perceptron menggunakan back propagation. Di postingan ini, saya akan menggunakan Theano dalam mengimplementasi perceptron.

Training Perceptron Menggunakan BackPropagation

Tujuan utama dalam proses training adalah meminimalisir error atau perbedaan antara output yang diharapkan (desired output) dan output sebenarnya yang dihasilkan oleh perceptron (actual output). Dalam hal ini kita dapat menggunakan algoritma seperti backpropagation. Cara kerja algoritma backpropagation sendiri adalah dengan mengubah nilai weights pada sebuah perceptron secara iterative berdasarkan nilai error hingga nilai error mencapai batas tertentu. Secara umum terdapat tiga tahapan pada BackPropagation.

Forward Propagation: Pada tahap ini input akan diberikan kepada perceptron, dap perceptron akan menghasilkan output berdasarkan input tersebut.
Error Calculation: Perbedaan antara actual output dan desired output dikalkulasi menggunakan sebuah fungsi error (contoh: root mean square atau croos entropy)
Backpropagation: Merubah nilai weight pada perceptron berdasarkan nilai error pada tahan ke dua.

Ok pada bagian ini saya akan menjabarkan secara singkat tentang ketiga tahapan diatas.

Forward Propagation

Tahap forward propagation adalah proses dimana perhitungan output perceptro berdsarkan input yang diberikan. Hal ini dapat diselesaikan dengan formula dibawah:

Untuk $x = input, y = output, W = weights, \sigma(.) = output \ function$ .

$z = \sum_{n} w_i x_i = W^T x$
$y = \sigma (z)$

dimana

$y = \sigma(z) = \dfrac{1} {1 + e ^ {-z}}$

$\frac{\partial y}{\partial z} = -1(1 + e ^ {-z}) ^ {-2} = \dfrac{1}{1 + e ^ {-z}} \dfrac{e^{-z}}{1 + e^{-z}} = y(1 - y)$

Pada tutorial ini saya menggunakan fungsi Sigmoid sebagai fungsi keluaran perceptron dikarenakan nilai output yang saya harapkan adalah 0 atau 1.

Note:

BP tidak dapat digunakan pada perceptron dengan binary threshold sebagai fungsi output, dikarenakan turunan binary threshold terhadap nilai z = 0 ( $\frac{\partial y}{\partial z} = 0$ )

$y =\begin{cases}1, & z \geq {threshold}\\0, & \text{otherwise} \\ \end{cases}$

Error Calculation

Setelah mendapatakan output dari perceptron berdasarkan input yang diberikan, pada tahap error calculation perceptron akan dievaluasi “apakah output perceptron sesuai dengan output yang diharapkan atau tidak”. Untuk menghitung perbedaan antara actual output dan desired output dapat digunakan berbagai macam fungsi error seperti Squared Error, Root Mean Squared Error (RMSE), Cross Entropy, atau Cosine Proximity. Dalam tutorial ini saya akan menggunakan Squared Error(untuk memudahkan proses perhitungan BP)

Untuk

$t = actual \ output, t \in {0 ~ 1} \\ y = desired \ output , y \in {0 \ atau \ 1}, dan \\ N = jumlah \ data$

Squared error dari t dan y dapat dihitung menggunakan formula

$E = \dfrac{1}{2} \sum\limits_{i=1}^N (t_i - y_i)^2$

dimana

$\frac{\partial E}{\partial y} = \dfrac{2}{2} \Sigma (t_i - y_i)^2 * -1 = - \Sigma (t_i - y_i)$

Note:

Error fungsi juga dikenal dengan nama cost function dan objective function.

Back Propagation

Secara umum proses learning pada neural network adalah dengan mengubah nilai weights berdasarkan error yang dibuat network tersebut dalam memprediksi data yang diberikan. Proses learning pada network dapat diformulasikan dengan formula

$w_{new} = w_{old} - \Delta w$

dimana,

$\Delta w = \pm x$

Kondisi:

Jika output benar, maka $\Delta w = 0$
Jika output salah (t =0 tetapi y = 1), maka $\Delta w = -x$
Jika output salah (t =1 tetapi y = 0), maka $\Delta w = +x$

Pada backpropagation proses learning tidak berdasarkan desired output, namun berdasarkan turunan fungsi error $\frac{\partial E}{\partial z}$ .

$\frac{\partial E}{\partial z_i} = \frac{\partial y_i}{\partial z_i} \frac{\partial E}{\partial y_i}$

$\frac{\partial E}{\partial z_i} = -y_i(1-y_i) (t_i - y_i)$

$\frac{\partial E}{\partial w_i} = \frac{\partial z_i}{\partial w_i} \frac{\partial E}{\partial z_i}$

$\frac{\partial E}{\partial w_i} = x_i\frac{\partial E}{\partial z_i}$

Sehingga,

$\Delta w = \varepsilon \frac{\partial E}{\partial w_i}$

$\varepsilon = learning \ rate$

Note:

Learning rate menentukan seberapa besar nilai weights akan berubah. Semakin kecil nilai learning rate, maka proses training akan semakin lama tapi perceptron akan dapat memahami lebih baik. Analogi (learning rate = tinggi = sistem kebut semalam, learning rate = kecil = belajar bertahap)

Implementasi menggunakan Theano

Pada tutorial ini saya akan menggunakan perceptron untuk menyelesaikan permasalahan gerbang logikal AND.

INPUT		OUTPUT
A	B	A AND B
0	0	0
0	1	0
1	0	0
1	1	1

Memodelkan perceptron dengan Theano

Langkah pertama dalam mengimplementasikan perceptron menggunakan Theano adalah mendefinisikan variable tensor.

#input
X = T.dmatrix('x')
#desired output
t = T.ivector('t')

Untuk variable weights dan bias, tidak hanya didefinisikan namun kita juga harus menginisialisasi nilai awal variable tersebut. Untuk weights saya menggunakan nilai random dengan limit $[-4 \sqrt{\frac{6}{nInput + nOutput}}, 4 \sqrt{\frac{6}{nInput + nOutput}}]$ (ref: 2), dimana $nInput$ = jumlah neuron pada layer input (nOutput = 2) dan $nOutput$ = jumlah neuron pada layer output (nOutput = 1). Sedangkan nilai bias diinisialisasi dengan nilai 0

bound = 4 * (6./np.sqrt(nInput + nOutput))
#weights
W = theano.shared(value=rng.uniform(low=-bound, high=bound, size=(nInput, nOutput)))
#bias
b = theano.shared(value= np.zeros(nOutput))

Pada tutorial ini saya menggunakan sigmoid sebagai activation function pada output layer. Pada theano terdapat build-sigmoid function sehingga kita tidak perlu membuat dari scratch.

#T.dot(a,b) = dot product dari variable a dan b
y = T.nnet.sigmoid(T.dot(X, W) + b)

Implementasi Squared Error

Setelah berhasil memodelkan perceptron, langkah selanjutnya adalah dengan membuat fungsi untuk menghitung error. Saya menggunakan squared error untuk menhitung perbedaan actual output dan desired output.

def SE(t, y):
 return T.sum(T.power(t - y.T, 2))/2

Implementasi BackPropagation

Seperti dijelaskan sebelumnya, bahwa untuk mentrain perceptron menggunakan BackPropagation, nilai weights dan bias akan diubah berdasarkan derivative error function (cost function) terhadap variable yang bersangkutan. $\frac{\partial E}{\partial w}$ adalah derivative error terhadap weights, dan $\frac{\partial E}{\partial b}$ adalah derivative error terhadap bias.

Pada Thenao, untuk menghitung derivative terhadap sebuah variable, kita dapat menggunakan fungsi T.grad().

cost = SE(t, y)
#gradient cost function terhadap variable W
gW = T.grad(cost, W)
#gradient cost function terhadap variable b
gB = T.grad(cost, b)

Setela menghitung nilai $\frac{\partial E}{\partial w}$ dan $\frac{\partial E}{\partial b}$ kita dapat mengupdate nilai W dan b dengan formula

$w_{new} = w_{old} - \Delta w$

$b_{new} = b_{old} - \Delta b$

Implementasi formula diatas pada theano dapat dilakukan dengan mengexpresikan formula diatas pada sebuah variable

updates = [(W, W - learningRate * gW), (b, b - learningRate * gB)]

(W, W – learningRate * gW) memiliki arti $w_{new} = w_{old} - \Delta w$ .

Wrap Everything

Langkah terakhir dalam mengimplementasikan perceptron pada Theano adalah dengan menyatukan model diatas pada sebuah fungsi. Pada tahap ini, kita akan mendefinisikan sebuah fungsi Theano yang akan menyatukan ekspresi – ekspresi diatas.

trainModel = theano.function(inputs=[X, t], outputs=cost, updates=updates)
testModel = theano.function(inputs=[X], outputs=pred)

trainModel adalah fungsi yang akan digunakan untuk mentrain perceptron, dimana input fungsi tersebut adalah X dan t (desired output), sedangkan outputnya adalah cost atau error function. Pada fungsi ini dijelaskan juga tentang variable yang akan diupdate setiap fungsi ini dijalankan.

testModel adalah fungsi yang akan digunakan untuk mentest perceptron, dimana input funsi tersebut adalah X dan outputnya adalah nilai prediksi terhadap input yang diberikan.

Train Perceptron

Untuk mentrain perceptron, kita hanya perlu memanggil fungsi trainModel, jika ingin mentrain perceptron sebanyak 100 iterasi kita hanya perlu memanggil fungsi tersebut sebanyak 100 kali. Hal tersebut dapat diimplementasikan dengan mudah menggunakan loop.

for i in range(100):
 err = trainModel(inputX, desiredOutput)

Atau jika ingin mentrain model hingga error function dibawah batas tertentu kita dapat menggunakan while.

err = 1
while err > 0.5
 err = trainModel(inputX, desiredOutput)

Note:

Penggunakan error fungsi tergantung dengan permasalahan yang ingin dimodelkan dengan ANN, apakah itu regresi, binary-classification, atau multiclasses-classification

Full Code

import theano
import theano.tensor as T
import numpy as np
def SE(t, y):
return T.sum(T.power(t - y.T, 2))/2
inputX = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
desiredOutput = np.array([0, 0, 0, 1])
rng = np.random.RandomState(5145022)
nInput = 2
nOutput = 1
iterationStep = 1000
learningRate = 0.1
X = T.dmatrix('x')
t = T.ivector('t')
bound = 4 * (6./np.sqrt(nInput + nOutput))
W = theano.shared(value=rng.uniform(low=-bound, high=bound, size=(nInput, nOutput)))
b = theano.shared(value= np.zeros(nOutput))
y = T.nnet.sigmoid(T.dot(X, W) + b)
pred = y > 0.5
cost = SE(t, y)
gW = T.grad(cost, W)
gB = T.grad(cost, b)
updates = [(W, W - learningRate * gW), (b, b - learningRate * gB)]
trainModel = theano.function(inputs=[X, t], outputs=cost, updates=updates)
testModel = theano.function(inputs=[X], outputs=pred)
err = 1
errList = np.zeros(iterationStep)
for i in range(iterationStep):
err = trainModel(inputX, desiredOutput)
errList[i] = err
print(testModel(inputX))

Referensi

Rosenblatt, Frank. “The perceptron: A probabilistic model for information storage and organization in the brain.” Psychological review 65.6 (1958): 386.
Glorot, Xavier, and Yoshua Bengio. “Understanding the difficulty of training deep feedforward neural networks.” Aistats. Vol. 9. 2010.

Apakah itu Perceptron?

Training Perceptron Menggunakan BackPropagation

Forward Propagation

Error Calculation

Back Propagation

Implementasi menggunakan Theano

Memodelkan perceptron dengan Theano

Implementasi Squared Error

Implementasi BackPropagation

Wrap Everything

Train Perceptron

Full Code

Referensi

About the Author

Leave a Reply Cancel reply