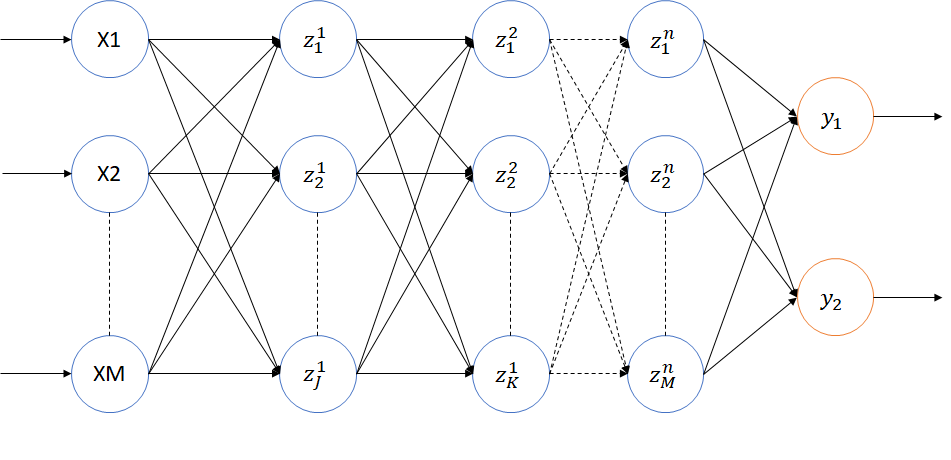
Konsep Multi Layer Perceptron Menggunakan Tensorflow pada Kasus Diagnosis Kanker Payudara

Multi Layer Perceptron

ilustrasi — Apa itu Multi Layer perceptron?

Multi-layer perceptron adalah perceptron dengan satu atau lebih hidden layer, dimana input sebuah perceptron adalah output dari perceptron sebelumnya. Tidak seperti perceptron yang hanya dapat memodelkan permasalahan linear, multi-layer perceptron juga dapat menyelesaikan permasalahan non-linear.

Walapun secara teori sebuah MLP adalah sebuah neural network model dengan satu atau lebih hidden layer, pada implementasinya sangatlah jarang ditemukan multi-layer perceptron dengan hidden layer lebih dari tiga (sebelum konsep Deep NN ditemukan). Hal tersebut dikarenakan kesulitan dalam proses latihan multilayer perceptron dengan lebih dari tiga hidden layer. Permasalahan yang biasa dialami oleh multi-layer perceptron yang memiliki lebih dari tiga hidden layer adalah vanishing/exploding gradient.

Vanishing/exploding gradient disebabkan oleh unstable gradient pada neural network. Pada sebuah neural network yang memiliki banyak hidden layer, nilai gradient pada layer awal dapat menjadi sangat besar ataupun sangat kecil. Hal tersebut dikarenakan proses learning pada layer terdahulu lebih lambat dari layer sebelumnya. Permasalahan vanishing/exploding gradient adalah permasalahan yang tidak dapat dielakan oleh ANN dengan deep hidden layer.

Baru-baru ini kita sering mendengar konsep Deep Neural Network (DNN), yang merupakan re-branding konsep dari Multi Layer Perceptron dengan dense hidden layer [1]. Pada Deep Neural Network permalahan seperti vanishing / exploding gradient telah dapat diatasi sehingga untuk menlatih ANN dengan hidden layer lebih dari tiga sangatlah memungkinkan.

Kesuksesan dari DNN sendiri tidak hanya didukung oleh penemuan teknik komputasi untuk DNN, namun juga didukung dengan meningkatnya jumlah data yang tersedia untuk melatih DNN dan kapasitas hardware yang memungkinkan. Beberapa penemuan teknik komputasi DNN adalah aktivasi fungsi ReLu dan fungsi Cross Entropy Loss.

ReLu

ReLu[4] merupakan sebuah aktifasi fungsi yang mengeluarkan output 0 jika nilai $x = 0$ , jika tidak nilai keluaran adalah nilai $x$ itu sendiri.

$f(x) = max(0, x)$

$f(x) =\begin{cases}0, & \text{if } x < 0\\x, & \text{otherwise} \\ \end{cases}$

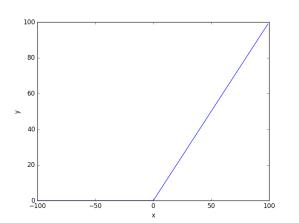
Aktivasi Fungsi Relu — Plotting relu dengan nilai x = [-100 ~ 100]

Turunan dari fungsi ReLu dapat diekspresikan dengan $f(x) =\begin{cases}0, & \text{if } x < 0\\1, & \text{otherwise} \\ \end{cases}$

Turunan fungsi relu — **Graph dari turunan aktifasi fungsi ReLu**

Keunggulan ReLu
- Dibandingkan dengan sigmoid dan hard tanh, operasi pada fungsi ReLu lebih simpel dikarenakan implementasi ReLu dapat dilakukan dengan menggunakan threshold pada nilai 0. Selain itu, dikarenakan gradient dari ReLu adalah 1 atau 0 maka neuron dengan ReLu tidak akan mengalami vanishing gradient dikarenakan nilai gradient yang tidak akan saturate.
- Pada beberapa paper ditemukan bahwa neural network model menggunakan ReLu dapat mencapai konvergen lebih cepat dibandingkan dengan model dengan sigmoid ataupun tanh
Permasalahan dalam ReLu
- Walaupun relu tidak mengalami permasalahan vanishing gradient dan dapat mempercepat neural network model untuk mencapai konvergen, fungsi ReLu dapat menyebabkan masalah “dying neuron”. Hal tersebut akan terjadi ketika gradient dengan nilai yang besar melewati neuron dengan ReLu dan nilai weight diupdate berdasarkan nilai gradient tersebut.

$w_{t} = w_{t-1} - \eta \nabla F(w_{t-1})$

Hal ini akan menjadikan sebagian besar output keluaran neuron tersebut bernilai negatif yang mana pada fungsi ReLu akan bernilai 0.

Cross Entropy

Berbeda dengan artikel sebelumnya mengenai linear regressi, dimana squared error digunakan untuk menghitung error antara predicted output dan actual output, pada artikel ini akan digunakan cross entropy [3]. Hal ini dikarenakan permasalahan pada penggunaan squared error bila diimplementasikan pada kasus klasifikasi dengan logistik output.

Telah diketahui sebelumnya bahwa nilai gradient berdasarkan fungsi squared error tehadap nilai $w_i$ dengan logistik output adalah

$\frac{\partial E}{\partial w_i} = - x_i y_i(1-y_i) (y_i - a_i)$

Dapat dilihat dari formula diatas bahwa nilai $(1-y_i)$ akan mendekati 0 ketika nilai predicted output $y$ mendekati 1. Sebagai contoh, jika $y$ mendekati 1 (y = 0.99999) dan nilai actual ouput $a$ adalah 0, maka nilai gradient adalah $\simeq 0$ .

$= - x_i * 0.99999(1-0.99999)(0.99999- 0)$

Hal tersebut dapat mengakibatkan proses latihan terjebak didalam plateau, dikarenakan nilai gradient update yang sangat kecil. Sedangkan pada kasus diatas seharusnya terdapat nilai gradient update yang cukup besar karena nilai predicted output $y = 0.99999$ berbeda dengan nilai actual output $a = 0$ .

Berbeda dengan squared error, cross entropy tidak mengalami permasalahan seperti diatas. Pada cross entropy semakin besar kesalahan prediksi ANN maka akan semakin besar nilai update terhadap weight. Fungsi error cross entropy dapat diformulasikan sebagai berikut

$E = - \frac{1}{N}\sum_{i=1}a_i log (y_i)+(1 - a_i)log(1-y_i)$

dimana $y_i$ adalah keluaran neuron ke ith, $a_i$ adalah actual output ke ith, dan $N$ adalah jumlah total dataset. Sedangkan turunan untuk cross entropy dengan fungsi output logistik terhadap $w_i$ adalah

$\frac{\partial E}{\partial w_i} = \frac{\partial z}{\partial w_i}\frac{\partial y_i}{\partial z_i}\frac{\partial E}{\partial y_i} = - x_i y_i(1-y_i) \frac{a_i(1-y_i) - (1 - a_i)y_i}{y_i(1 - y_i)} = - x_i(y_i - a_i)$

Jika dilihat dari formula diatas, dapat disimpulkan bahwa besaran gradient update pada ANN model dengan error fungsi cross entropy akan ditetukan dengan nilai perbedaan antara predicted output dan actual output $(y_i - a_i)$ . Semakin besar perbedaan antara keduanya, semakin besar nilai update pada weight neuron. Sebagai contoh, jika nilai $y_i = 0.99999$ sedangkan nilai $a_i = 0$ , maka besaran nilai gradient update adalah $x_i * 0.9999$ .

Full Implementasi

Dalam artikel kali ini, saya akan mengimplementasikan multilayer perceptron dengan lima hidden layer pada kasus diagnosis kanker payudara menggunakan Breast Cancer Wisconsin dataset. Wisconsin dataset sendiri terdiri dari 9 input features dan 2 output (benign atau malignant). Input features merupakan hasil perhitungan dari sebuah digitized image of a fine needle aspirate (FNA) dari berat sebuah payu dara. Untuk penjelasan dataset dapat dilihat disini.

Struktur dari neural network model yang digunakan dalam artikel ini terdiri dari:

Input Layer: 9 units
Hidden Layer 1: 1024 output units (aktivasi fungsi: ReLu / Sigmoid)
Hidden Layer 2: 1024 output units (aktivasi fungsi: ReLu / Sigmoid)
Hidden Layer 3: 2048 output units (aktivasi fungsi: ReLu / Sigmoid)
Hidden Layer 4: 2048 output units (aktivasi fungsi: ReLu / Sigmoid)
Hidden Layer 5: 2048 output units (aktivasi fungsi: ReLu / Sigmoid)
Output Layer: 2 units (aktivasi fungsi: Logistic)

ANN Model struktur — Ilustrasi struktur ANN Model yang terdiri dari 5 hidden layers.

Pada implementasi kali ini, TensorFlow akan digunakan sebagai framework dalam memodelkan ANN. Tidak digunakannya Theano pada artikel ini dikarenakan pengembangan Thenao telah diberhentikan (detail).

Langkah pertama dalam implementasi ini adalah membuat fungsi untuk mendefinisikan model. Terdapat tiga variabel dalam fungsi tersebut, features, label, dan mode. Features adalah parameter untuk input feature. Labels adalah parameter untuk actual outputs. Sedangkan mode adalah parameter untuk mendefinisikan running mode, apakah train, eval, atau prediction.

# mendefinisikan ANN model
def my_model(features, labels, mode):

Pada implementasi ini ANN model akan memiliki struktur seperti penjelasan sebelumnya. Untuk menginisialisasi nilai weight pada model digunakan fungsi Xavier [5]. Dan pada input layer seluruh input akan di-reshape kedimensi [n, 9] dimana n adalah jumlah batch_size atau jumlah data untuk setiap epoch, nilai -1 mengindikasikan bahwa nilai batch_size tidak diinisialisasi.

# fungsi xavier untuk inisialisasi weight neural network
# ref: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.207.2059&amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;rep=rep1&amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;type=pdf
init = tf.contrib.layers.xavier_initializer()
# aktivasi untuk hidden output units
activation = tf.nn.sigmoid
# definisikan sebuah tensor untuk input layer yg berdimensi 9
# -1 (belum didefinikan) adalah dimensi untuk jumlah batch
input_layer = tf.reshape(features["x"], [-1, 9])
# layer 1 dengan input adalah output dari input layer
# layer 1 memiliki 1024 output units dengan aktifasi sesuai dengan nilai variable activation
layer1 = tf.layers.dense(inputs=input_layer, units=1024, activation=activation, kernel_initializer=init,
name="layer1")
# layer 2 dengan input adalah output dari layer 1
# layer 2 memiliki 1024 output units dengan aktifasi sesuai dengan nilai variable activation
layer2 = tf.layers.dense(inputs=layer1, units=1024, activation=activation, name="layer2")
# layer 3 dengan input adalah output dari layer 2
# layer 3 memiliki 2048 output units dengan aktifasi sesuai dengan nilai variable activation
layer3 = tf.layers.dense(inputs=layer2, units=2048, activation=activation, name="layer3")
# layer 4 dengan input adalah output dari layer 3
# layer 4 memiliki 2048 output units dengan aktifasi sesuai dengan nilai variable activation
layer4 = tf.layers.dense(inputs=layer3, units=2048, activation=activation, name="layer4")
# layer 5 dengan input adalah output dari layer 4
# layer 5 memiliki 2048 output units dengan aktifasi sesuai dengan nilai variable activation
layer5 = tf.layers.dense(inputs=layer4, units=2048, activation=activation, name="layer5")
# output layer dengan input adalah output dari layer 5
# output layer memiliki 2 output units
logits = tf.layers.dense(inputs=layer5, units=2)
# menghitung probability terhadap seluruh kelas (benign atau maligant) berdasarkan input yang diberikan
prob = 1 / (1 + tf.exp(-logits))

Pada baris code diatas telah diimplementasikan ANN model sesuai dengan struktur yang dijelaskan sebelumnya. tf.layer.dense adalah sebuah tensor pada Tensorflow yang mendifinisikan feed-forward neural network, yang dapat digunakan sebagai (hidden/output) layer. Pada tensor logits parameter activation = None yang mana memiliki arti fungsi linear digunakan pada layer tersebut.

Tahap selajutnya adalah mendifinisikan aksi untuk setiap mode, train, eval, dan predict. Untuk setiap mode dapat didefinisikan nilai keluaran yang berbeda dengan mendifinisikan nilai paramater pada EstimatorSpec. Perlu diperhatikan bahwa pada Tensorflow sebuah fungsi yang medifinisikan ANN model harus memiliki output balikan class EstimatorSpec yang digunakan sebagai input untuk fungsi Estimator yang digunakan dalam proses melatih dan mengevaluasi model.

# prediksi dari model terdiri dari 2 units, class dan probability
# classes adalah index dari output units dengan nilai terbesar
# contoh jika nilai output units adalah [0.5, 0.3] maka classes adalah 0
predictions = {
"classes": tf.argmax(logits, axis=1),
"probabilities": prob
}
#aksi untuk mode predict
if mode == tf.estimator.ModeKeys.PREDICT:
return tf.estimator.EstimatorSpec(mode=mode, predictions=predictions)
# merubah output menjadi onehot_labels
# contoh jika depth = 2, maka untuk nilai 1 = [1 0] dan nilai 2 = [0 1]
onehot_labels = tf.one_hot(indices=tf.cast(labels, tf.int32), depth=2)
# meghitung cross entropy error
loss = -tf.reduce_mean(tf.cast(onehot_labels, tf.float64) * tf.log(prob) + (1.-tf.cast(onehot_labels, tf.float64)) * tf.log(1. - prob))
if mode == tf.estimator.ModeKeys.TRAIN:
#pada proses training digunakan metode Gradient Descent dengan learning rate 0.01
optimizer = tf.train.GradientDescentOptimizer(learning_rate=0.01)
train_op = optimizer.minimize(loss=loss, global_step=tf.train.get_global_step())
return tf.estimator.EstimatorSpec(mode=mode, loss=loss, train_op=train_op)
# evaluasi matrix saat proses validasi
eval_metric_ops = {
"accuracy": tf.metrics.accuracy(labels=labels, predictions=predictions["classes"])
}
return tf.estimator.EstimatorSpec(mode=mode, loss=loss, eval_metric_ops=eval_metric_ops)

Setelah mendefinisikan ANN model, tahap terakhir adalah mendefinisikan dan menetapkan nilai tensor variable untuk input features dan labels. Pada implementasi ini Pandas library digunakan untuk me-manage dataset yang disimpan dalam file CSV.

# read dataset dalam bentuk CSV
data = pd.read_csv("data\\breast-cancer-wisconsin.csv")
# ambil data berdasarkan kolom pada DataFrame
# X = features input
# y = labels
X = data[["clump_thickness", "uniformity_of_cellsize", "uniformity_of_cell_shape", "marginal_adhesion", "single_epithelial_cell_size", "bare_nuclei", "bland_chromatin", "normal_nucleoli", "mitoses"]].values.astype("float64")
y = data["class"].values
# lakukan proses splitting untuk data train dan validasi
# 70% training dan 30% evaluasi
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
# definisikan tensor untuk data train dan validasi
# pada proses training urutan data akan disuffel untuk setiap iterasi
# hal tersebut dilakukan untuk meningkatkan generalisasi performance dari ANN model
train_fn = tf.estimator.inputs.numpy_input_fn({"x": X_train}, y_train, num_epochs=1, shuffle=True)
eval_input_fn = tf.estimator.inputs.numpy_input_fn({"x": X_test}, y_test, num_epochs=1, shuffle=False)
# definisikan Estimator model dimana mode_fn adalah fungsi yang telah kita definisikan sebelumnya
# dan model_dir adalah directory untuk menyimpan model dan log dari model
estimator = tf.estimator.Estimator(model_fn=my_model, model_dir="./tmp/model(lr=0.001)_sign_grad")
# lakukan proses training sebanyak 300 iterasi
train_spec = tf.estimator.TrainSpec(input_fn=train_fn, max_steps=300)
# lakukan proses evaluasi atau validasi untuk setiap iterasi
eval_spec = tf.estimator.EvalSpec(input_fn=eval_input_fn)
# lakukan eksekusi untuk proses training dan validasi
tf.estimator.train_and_evaluate(estimator, train_spec, eval_spec)

Hasil Eksprimen

Dalam eksperimen ini ANN model dilatih dengan learning rate 0.01* dan iterasi sebanyak 300. Dataset dibagi menjadi dua bagian, training (70%) dan validasi (30%). Training error dan validasi error diestimasi dengan fungsi cross-entropy. Selain itu, akurasi performance dari model dievaluasi dengan validasi data pada setiap iterasi.

*Note: nilai learning rate akan sangat mempengaruhi hasil dari proses training, pemilihan nilai learning rate pada artikel ini dilakukan beberapa kali secara random. 0.01 adalah nilai yang terbaik yang didapatkan dalam eksperimen ini.

Error Loss

Berdasarkan grafik 1 dapat dilihat bahwa training dan validasi error ANN model menggunakan aktivasi fungsi ReLu pada hidden layer menurun secara berangsur pada setiap iterasi. Pada iterasi awal nilai dari training error dan validasi error berkisar diangka 0.68 dan terus menurun hingga mencapai nilai 0.25 pada akhir iterasi.

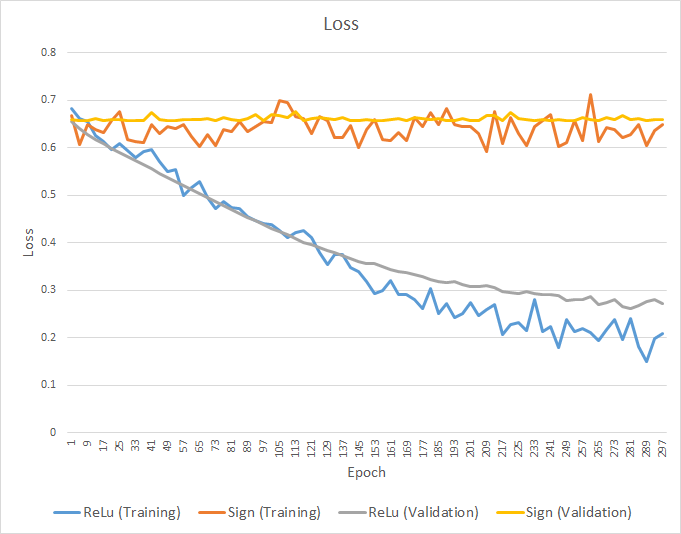
Disisi lain, training error dan validasi error dari ANN model dengan aktivasi fungsi Sigmoid tidak mengalami proses penurunan yang signifikan dari proses awal training. Pada iterasi awal nilai training dan validasi error berkisar pada nilai 0.66 dan berakhir pada kisaran nilai 0.65.

Dari hasil diatas, dapat disimpulkan bahwa penggunaan aktivasi fungsi ReLu pada hidden units meningkatkan performa dari proposed ANN model. Hal tersebut dikarenakan ANN model dengan ReLu memiliki kemungkinan yang lebih kecil untuk mengalami vansihing gradient yang biasa dialami oleh multilayer perceptron dengan deep hidden layer yang menggunakan aktivasi fungsi sigmoid atau tanh pada hidden units. ANN model dengan ReLu dapat melakukan proses trainining yang lebih baik dikarenakan komputasi gradient yang tidak mengalami proses saturation.

Akurasi

Untuk mengevaluasi performa generalisasi dari ANN model pada kasus klasifikasi, sebuah model harus diuji untuk memprediksi unseen data. Seperti dijelaskan pada sebelumnya bahwa pada eksperimen ini, akurasi dari proposed model juga dihitung untuk setiap iterasi menggunakan validasi data.

Pada grafik 2 ditampilkan akurasi dari ANN model dengan ReLu atau Sigmoid aktivasi fungsi. Pada iterasi awal, akurasi dari ANN model dengan ReLu adalah 38.04% dan meningkat secara berkelanjutan pada setiap iterasi. Akurasi tertinggi dari ANN model dengan ReLu mencapai nilai 92.19 pada akurasi ke-268.

Berbeda dengan ReLu, akurasi dari ANN model dengan sigmoid pada hidden unitsnya tidak cukup memuaskan. Akurasi stagnan pada nilai 61.95% dari iterasi awal hingga iterasi akhir. Hal tersebut mengindikasikan terjadinya vanishing gradient, dimana proses pembelajaran pada model tidak terjadi pada keseluruhan layer ANN model.

Kesimpulan

Untuk melatih sebuah ANN model dengan deep hidden layer tidaklah mudah. Sebuah ANN dengan deep hidden layer dapat dengan mudah mengalami permasalahan vanishing\exploding gradient. Penemuan teknik komputasi seperti fungsi aktifasi ReLu dan fungsi error Cross Entropy dapat meminimalisir kemungkinan sebuah deep ANN untuk mengalami vanishing gradient. Pada artikel ini sebuah neural network dengan lima hidden layer digunakan untuk memodelkan permasalahan diagnosis kanker payu dara. Dari hasil eksperimen ditemukan bahwa ANN model dengan ReLu aktivasi fungsi memiliki performa yang lebih unggul dibanding dengan ANN model dengan sigmoid fungsi. Walaupun akurasi dari ANN model dengan ReLu memiliki performa yang menjanjikan (akurasi > 90%) namun pengembangan dari proposed model masih bisa dapat dilakukan.

Download

Source code dari implementasi diatas dapat didownload disini

Referensi

[1] LeCun, Y., Bengio, Y., & Hinton, G. (2015). Deep learning. Nature, 521(7553), 436-444.

[2] https://www.cs.toronto.edu/~tijmen/csc321/slides/lecture_slides_lec6.pdf

[3] http://www.deeplearningbook.org/

[4] Nair, V., & Hinton, G. E. (2010). Rectified linear units improve restricted boltzmann machines. In Proceedings of the 27th international conference on machine learning (ICML-10) (pp. 807-814).

[5] Glorot, X., & Bengio, Y. (2010, March). Understanding the difficulty of training deep feedforward neural networks. In Proceedings of the Thirteenth International Conference on Artificial Intelligence and Statistics (pp. 249-256).

Disarikan dari https://prasetiautamacv.wordpress.com/2018/01/07/multi-layer-perceptron-menggunakan-tensorflow-pada-kasus-diagnosis-kanker-payudara/